• letzte Änderung: 13.10.2006
• Größe: 484 KB

Falls Sie Probleme haben das Applet auszuführen, lesen Sie bitte hier, welche Voraussetzungen ihr Browser haben muss, um unsere Applets anzeigen zu können.

Dieses Applet visualisiert Riemannsummen von Funktionen in zwei Variablen. Durch den Graphen einer Funktion z=f(x,y) wird eine Fläche im Raum definiert. Das Integral der Funktion z=f(x,y) kann mit verschiedenen numerischen Integrationsverfahren berechnet werden. Der errechnete Wert, der Fehler zum tatsächlichem Wert und der Wert des Integrals werden ausgegeben. Die Fläche im Raum und die Approximation durch Treppenfunktionen werden visualisiert.
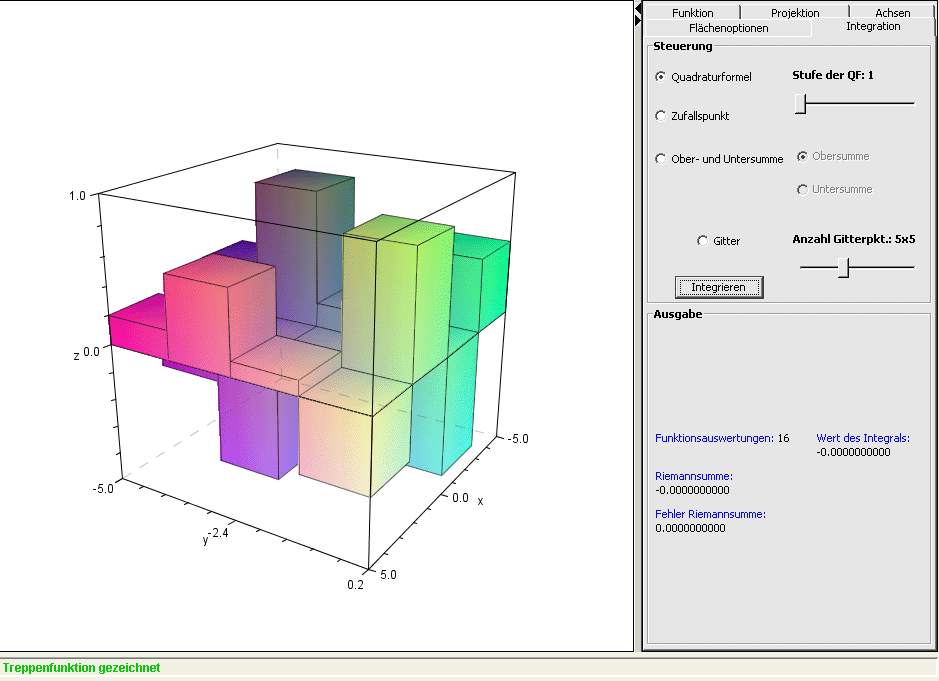
Für eine schnelle und einfache erste Visualisierung einer Riemannsumme einfach unter Beispiel eine Funktion auswählen. Den Button Zeichnen drücken. Jetzt wird der Graph der Funktion dargestellt. Im Reiter Integration kann dann die Regel, nach der integriert werden soll, ausgewählt werden. Den Button Integration drücken. Jetzt wird die approximierende Treppenfunktion dargestellt. Im Reiter Flächenoptionen kann man im Menüfeld Sichtbarkeit zwischen Fläche und Treppenfunktion wechseln. Unter Flächenoptionen kann die Darstellung der Fläche und der Treppenfunktion getrennt verändert werden. Die Reiter Projektion und Achsen erweitern noch zusätzlich die Möglichkeiten der Darstellung.
Beispiele
Beim Klicken auf eines der Beispiele werden die Daten für verschiedene Funktionen übernommen.
Fläche definieren
Wie man im Screenshot sieht, wird die Funktion im Feld f(x,y) festgelegt. Nähere Informationen über die Syntax und die unterstützten Funktionen finden Sie hier. Mit Hilfe des Schiebereglers Anzahl Gitterpunkte geben Sie an, aus wie vielen Gitterpunkten die Fläche aufgebaut werden soll. In den Textfeldern, die mit Bereich beschriftet sind, setzen sie den (rechteckigen) Bereich in der xy-Ebene fest, über dem der Funktionsgraph gezeichnet werden soll.
Im Reiter Flächenoptionen kann man im Menüfeld Sichtbarkeit definieren, ob der Funktionsgraph oder der Graph der Treppenfunktion sichtbar ist. Die Optionen in der linken Spalte ändern den Funktionsgraph, die in der rechten Spalte ändern die Treppenfunktion. Neben der Anzahl der verwendeten Gitterpunkte können Sie im Reiter Flächenoptionen weitere Grundeinstellungen zur Darstellung der Fläche festlegen. Unter der Überschrift Flächenoptionen setzen Sie fest, ob die Fläche als Gitter oder mit "gefüllten" Facetten dargestellt wird. Unter Fülloptionen wählen Sie die Art, wie die Dreiecke, aus denen die Fläche aufgebaut wird, gefärbt werden sollen. Falls die Option einfach gewählt ist, wird das Dreieck mit der Farbe eines seiner Eckpunkte gefärbt, während bei der Option interpoliert die Farbe zwischen den Eckpunkten interpoliert wird. Unter Farbe finden Sie weitere Möglichkeiten, die Farbe der Fläche zu beeinflussen. Mit der Option z verändert die Fläche nur in z-Richtung ihre Farbe, mit der Option xy in x- und y-Richtung und mit der Option xyz in allen drei Richtungen. Mit der Option Vorder-Rückseite setzen Sie fest, dass die Fläche nur mit zwei Farben gezeichnet wird, nämlich mit einer für die Vorder- und einer für die Rückseite. Die Zugehörigkeit zu Vorder- oder Rückseite der einzelnen Dreiecke, aus denen die Fläche aufgebaut ist, wird dabei mit Hilfe des Normalvektors auf das jeweilige Dreieck entschieden. Schließlich können Sie unter Renderoptionen festlegen, ob die Fläche mit möglichst guter Qualität oder möglichst schnell gezeichnet werden soll. Unter dem Reiter Projektion gibt es verschiedene Möglichkeiten, die Abbildung der Fläche auf die Projektionsebene zu beeinflussen. Sie können mit den Optionen Perspektive und Parallelprojektion zwischen diesen beiden Projektionsarten wählen und im Falle der perspektivischen Projektion mit Hilfe des Minus- und Plusknopfes die Entfernung der "Kamera" von der Fläche verändern. Mit der Auswahlbox Projektionsebene können sie im Fall der Parallelprojektion die Projektionsebene auswählen. Mit dem Knopf Zurücksetzen setzen Sie die Projektionseinstellungen und die Lage der Fläche auf die Ausgangswerte zurück. Durch Ziehen der Maus mit gedrückter linker Maustaste (im Zeichenbereich) können sie die Fläche drehen.
Unter dem Reiter Achsen können Sie die Skalierung der Achsen je nach gewählter Option für jede Achse einzeln oder für alle zusammen verändern. Weiters können Sie mit den Optionen unter der Überschrift Achsenmodell festlegen, ob um die Fläche eine "Box" gezeichnet und ob diese beschriftet werden soll. Im Reiter Integration kann man im Menüfeld Steuerung definieren, nach welcher Regel integriert werden soll, und die numerische Integration durch das Drücken des Buttons Integrieren ausführen.
Ausgabe
Im Menüfeld Ausgabe werden die Ergebnisse der Integration ausgegeben: die Anzahl der Funktionsauswertungen, der Wert des Integrals, der mit der gewählten Regel errechnete Wert und der Fehler zum Wert des Integrals. Der Wert des Integrals wird mit einer äquidistanten Unterteilung mit jeweils zehn Gitterpunkten und der Gauß'schen Quadraturformel der Stufe acht berechnet.

Quadratformel
Bei der Option Quadraturformel wird die Funktion über jedem Rechteck mit der Gauß'schen Quadraturformel (der mit dem Slider daneben gewählten Stufe) integriert. Die Treppenfunktion ist so gewählt, dass ihr Integral über jedem Rechteck mit dem errechneten Wert übereinstimmt. Die Quadraturformel der Stufe 1 entspricht der Mittelpunktsregel.

Zufallspunkt
Bei der Option Zufallspunkt wird die Funktionsauswertung an einem zufällig im Rechteck gewählten Punkt vorgenommen. Der Funktionswert bildet dann die Höhe des Quaders.

Ober- und Untersumme
Bei der Option Ober- und Untersumme wird in jedem Rechteck das Maximum und das Minimum der Funktion berechnet. Das Maximum ist dann die Höhe des Quaders für die Obersumme, das Minimum die Höhe des Quaders für die Untersumme. Mit den Buttons Obersumme und Untersumme kann die entsprechende Treppenfunktion visualisiert werden. In der Ausgabe werden die Werte beider Summen ausgegeben.

Gitter
Durch die Aktivierung der Option Gitter wird die Partitionierung dargestellt, über die integriert wird. Dabei entspricht die horizontale Unterteilung der x-Achse und die der vertikalen der y-Achse. Die Unterteilungen und die Stützstellen können mit der Maus wie folgt verändert werden:
• Ziehen eines Punktes mit gedrückter linker Maustaste: Bewegen eines Punktes;
• Klicken eines Punktes mit der mittleren Maustaste: Löschen des Punktes;
• Klicken einer freien Stelle auf einer der beiden Unterteilungsachsen mit der rechten Maustaste: Hinzufügen eines Teilungspunktes.
   
Mit dem Slider daneben wird eine äquidistante Partitionierung mit der angegebenen Anzahl der Gitterpunkte generiert.
Falls Sie weitere Fragen zum Applet haben, uns Hinweise auf Fehler oder Kommentare zukommen lassen wollen, schreiben Sie uns bitte.