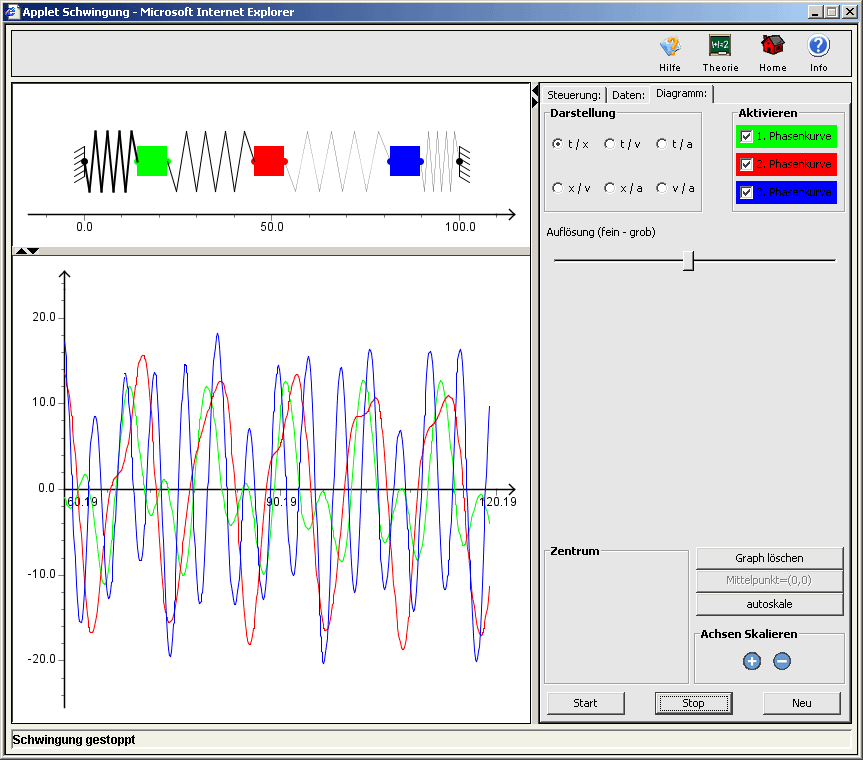
-
Für eine schnelle und einfache erste Visualisierung einer Schwingung einfach Beispiele eine Schwingung auswählen.
Den Button Neu drücken und mit dem Button Start die Animation starten.
Im Reiter Daten können dann die Daten variert werden. Im Reiter Diagramm kann noch die Darstellung der Phasenkurven, zum Beispiel Autoscale, verändert werden.
Beispiele
-
Beim Klicken auf eines der Beispiele werden die Daten für verschiedene Massenschwinger übernommen.
-
Die Darstellung ermöglicht es Ihnen, verschiedene Massenschwinger zu visualisieren. Zur Auswahl stehen:
eine Masse ... Massenschwinger mit einer Masse
zwei Massen ... Massenschwinger mit zwei Massen
drei Massen ... Massenschwinger mit drei Massen
nichtlinearer Massenschwinger ... Visualisiert einen Einmassenschwinger mit linearer und kubischer Rückstellkraft. Zusätzlich zu den Daten des linearen Anteils kann der Wert des Koeffizienten der kubischen Rückstellkraft eingegeben werden.
-
Die Zeitverzögerung verlangsamt die Animation beim Ziehen nach rechts.
Zeitverzögerung: 1 ... eine Sekunde der Animation entspricht einer Sekunde
Zeitverzögerung: 10 ... eine Sekunde der Animation entspricht einer zehntel Sekunden
-
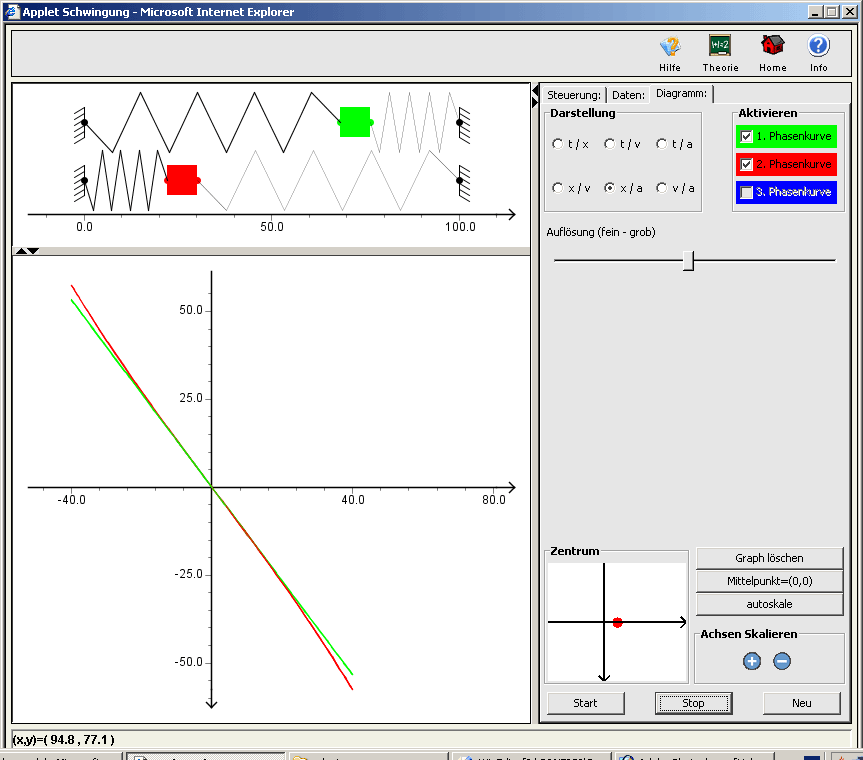
Bei der Schwingung von zwei Massen ist es möglich Linearkombinationen der beiden Zustandsvariablen darzustellen.
Hier kann man die Koeffizienten der Linearkombination in die zwei Datenfelder eingeben und die Option Phasenkurve der Linearkombination aktivieren, mit dem Button Neu übernehmen und mit dem Button Start die Animation starten.
Es wird dann im unteren Fenster die Phasenkurve der Linearkombination dargestellt.
Der Button Berechnen berechnet ihnen aus den eingegebenen Daten der Schwingung die Koeffizienten so, dass die Linearkombination der Phasenkurven eine harmonische Schwingung ergibt (Eigenschwingung).
Die berechneten Koeffizienten werden in den Datenfeldern ausgegeben.
-
Beim Klicken auf Start wird die Animation der Mehrmassenschwinger gestartet.
ACHTUNG: Eine Datenänderung erfordert das Drücken des Buttons Neu.
-
Beim Klicken auf Stop wird die Animation der Mehrmassenschwinger gestoppt.
ACHTUNG: Es werden keine Daten übernommen.
-
Beim Klicken auf Neu wird ein neues Mehrmassenschwinger erzeugt.
Zur Übernahme geänderter Daten muss immer der Button Neu gedrückt werden, anschließend Start.
Der Reiter Daten ermöglicht es Ihnen, die Daten für das Federpendel festzulegen. Je nachdem welche Option Sie
in der Darstellung aktiviert, haben können Sie bestimmte Daten festlegen. Die Datenfelder, die grau hinterlegt
sind, sind für die gewählte Feder-Massen-Kombination nicht erforderlich.
Masse 1,2,3
-
Masse des ersten, zweiten und dritten Massepunktes. Der Eingabewert muss größer null sein.
-
erste, zweite, dritte und vierte Federkonstante der Federn. Der Eingabewert muss größer null sein.
-
Anfangsposition des ersten, zweiten und dritten Massepunktes.
Bei der Schwingung einer Masse kann die Anfangsposition im Intervall [0,100](cm) ausgewählt werden.
Bei zwei und drei Massen kommen Einschränkungen der Anfangspositionen zum Tragen, da es sonst zu Kollisionen der Massen kommt, und damit der Gültigkeitsbereich des Modells überschritten würde.
Je nachdem wieviele Massenpunkte schwingen sollen wird das Intervall [0,100] gedrittelt oder geviertelt.
Diese Punkte sind dann die Mittelpunkte des zulässigen Intervalls für die Anfangspostionen.
Die maximalen Anfangsauslenkungen der Massen ergeben sich dann Minimum der Massen, multipliziert mit 100/6 oder 100/8.
Falls die eingegebene Position nicht im zulässigen Intervall liegt, wird unten links eine rote Fehlermeldung mit dem zulässigem Intervall ausgegeben.
-
Für jede Masse kann noch separat eine Dämpfung. Der Eingabewert muss größer null sein.
-
Im nichtlinearen Einmassenschwinger ist die Rückstellkraft die Summe des linearen und des kubischen Anteils.
Der Koeffizient des kubischen Terms kann als kubischer Beiwert eingegeben werden, und kann positiv oder negativsein. Realitätsnahe Werte ergeben sich bei plus, minus 10^-3. Achtung: Negative Beiwerte sind nur in einem beschränktem Bereich für das Modell zulässig.
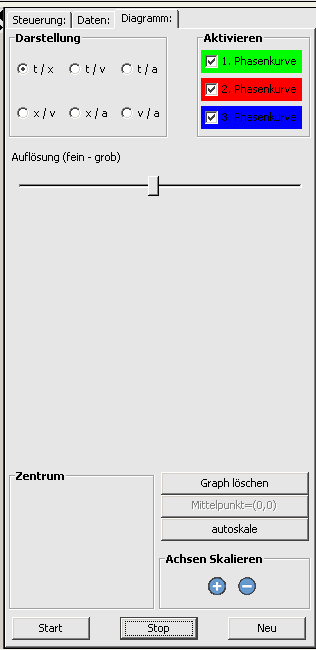
Darstellung
-
Zustands-Zeit-Diagramme:
t,x ... Zeit, Auslenkung
t,v ... Zeit, Auslenkungsgeschwindigkeit
t,a ... Zeit, Auslenkungsbeschleunigung
Phasendiagramme:
x,v ... Auslenkung, Auslenkungsgeschwindigkeit
x,a ... Auslenkung, Auslenkungsbeschleunigung
v,a ... Auslenkungsgeschwindigkeit, Auslenkungsbeschleunigung
-
Je nachdem welche Phasenkurve aktiviert ist wird sie auch mit der
jeweiligen Farbe im unteren Fenster dargestellt, denn gewählten Massenkombinationen entsprechend.
Während der Animation können Phasenkurve dazugeschalten oder weggeschalten werden.
Alle bisherigen Phasenkurven werden gelöscht und die aktivierten werden weitergezeichnet.
-
Die Auflösung kann bei leistungsschwachen Rechnern auf grob gesetzt werden um die Rechenzeit zu
verkürzen und so eine kontinuierliche Darstellung zu erhalten.
- Zentrum: Durch das Klicken auf einen beliebigen Punkt im darunter liegendem Quadrat können Sie den Mittelpunkt des Phasendiagramms verändern.
- Graph löschen: Löscht das Diagramm
- Mittelpunkt=(0,0): Setzt den Mittelpunkt des Diagramms auf (0,0)
- Autoscale: Skaliert das Diagramm so dass alle Gezeichneten Punkte sichtbar sind
- Achsen Skalieren:
... Vergrößert das Diagramm um den Mittelpunkt
... Verkleinert das Diagramm um den Mittelpunkt
Falls Sie weitere Fragen zum Applet haben, uns Hinweise auf Fehler oder Kommentare zukommen lassen wollen, schreiben Sie uns bitte.